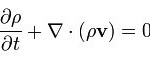Is there something wrong with the Navier-Stokes equations?
The Navier-Stokes Equations, above, are the fundamental equations of fluid dynamics. The first equation is Newton’s Second Law (F = ma) applied to a fluid and the second equation states mathematically that matter can neither be created nor destroyed. The equations are shown above in a highly compressed form using vector and tensor notation. When used for computation the equations expand, there being one equation for each dimension of three dimensional space. Further refinements are needed according to whether a description relative to a fixed grid (Eulerian) is required or one “moving with the fluid” (Lagrangian).
All computational fluid dynamics is based on these equations, such things as oceanographic modelling, weather prediction, climate modelling, the design of airframes, ships hulls, pumps, turbines and jet engines. They are a very powerful tool.
Powerful though they are, there are some aspects of fluid behaviour which are not well described by the equations. Chief among these is turbulent behaviour. So mysterious are the equations that the Clay Mathematical Institute has offered a $1 million “Millenium Prize” for the first person to solve certain mathematical aspects of the equations. As they state on their web site: “Although these equations were written down in the 19th Century, our understanding of them remains minimal. The challenge is to make substantial progress toward a mathematical theory which will unlock the secrets hidden in the Navier-Stokes equations.” See: http://www.claymath.org/millennium/Navier-Stokes_Equations/
Unfortunately the problem posed by the Clay Institute is purely mathematical; their statement of the problem assumes that the fluid is incompressible. Not only is this never the case in nature, it has the effect of being grossly non-realistic, because it means that any change in pressure “at infinity” is propagated instantaneously throughout the body of the fluid. Hence any solution to the Clay Institute problem, should one be found, will have little relevance to the behaviour of fluids in the real world.
A more fundamental and realistic issue, is the problem of turbulence. In 1941, the great Russian mathematician Andrey Kolmogorov, proposed the idea of a turbulent cascade, whereby interactions between vorticity and velocity gradients create ever smaller and smaller eddies until viscosity takes over. Kolomogorov based his prediction solely on dimensional arguments and ideas of self similarity. This prediction was not based on the Navier-Stokes equations! On the contrary, the Navier-Stokes equations are fundamentally incapable of making such a prediction.
The wavenumber spectrum of such a cascade is continuous and was predicted by Kolmogorov to have a power law slope equal to -5/3. This has since been observed experimentally. This continuous nature of the turbulent eddy spectrum indicates that it is the outcome of a stochastic (i.e. random) process and therefore cannot be derived from the Navier-Stokes equations which are deterministic.
This distinction is fundamental. Differential equations were devised by Newton and Liebniz in the seventeenth century to deal with the motion of large solid objects such as artillery shells and planets. Differential equations are deterministic, meaning that if you know the position of the shell or planet at one instant in time then you can predict it at the next then the next and so on. The variables in these equations represent numbers, fixed single quantities which change with position in space and time.
A century later, Laplace summarised this notion of causal determinism as follows: We may regard the present state of the universe as the effect of its past and the cause of its future. An intellect which at a certain moment would know all forces that set nature in motion, and all positions of all items of which nature is composed, if this intellect were also vast enough to submit these data to analysis, it would embrace in a single formula the movements of the greatest bodies of the universe and those of the tiniest atom; for such an intellect nothing would be uncertain and the future just like the past would be present before its eyes.
Laplace’s idea is, of course, nonsense. The function of numbers is for computation. To “know” the position of even a single particle with perfect precision requires a number with an infinite number of decimal places, far beyond the powers of any computing system either real or imagined. All quantities used in physical computations (other than simply counting) are approximations; there can be no real “real numbers”. Hence all numerical models must depart from reality after a certain number of time steps. Nevertheless Laplace’s wonderful but outmoded idea still seems to hold sway among applied mathematicians.
Around the beginning of the 20th century there were two huge paradigm shifts in Science. One was the theory of relativity. The other was the advent of quantum mechanics with its underlying idea that nature is fundamentally random. Out of this came a new sort of differential equation – stochastic equations in which the variables represent random variables rather than numbers. Each random variable carries with it a frequency distribution; in a sense each variable is seen as an approximation at the outset. This made it possible to derive the laws of thermodynamics from atomic theory, a major achievement.
The Navier-Stokes equations are not stochastic equations; that’s the problem. Because of their deterministic character, the Navier-Stokes equations cannot account for turbulence. The generation of turbulent eddies in the wake of a moving vessel is a random process. It is not possible for a deterministic model to generate such a random process. There must be some instant at which at least one deterministic path bifurcates. Thus an eddy is either formed or is not formed with a probability being assignable to each possible case. Such a bifurcation is not possible in a purely deterministic process such as that described by the Navier Stokes equations.
It might be argued that this problem can be overcome by randomising the boundary conditions and indeed this is precisely what is done with numerical climate models. The same version of the model is run many times from slightly different starting points. It is called an “ensemble”. Model runs are then averaged over the ensemble to give more precise predictions of output variables. The trouble is, this randomness is external to the model which remains a deterministic model internally. Despite this such models are frequently dealt with as if they were stochastic models even though they are not.
In summary then, it appears that the Navier-Stokes equations do not always provide a good description of the behaviour of real world fluids; they are not stochastic and it may well be that they are not complete.